正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるね一辺が1cmの正十二角形の内側に、1cmの正三角形が12個並んでいます。 このとき、色のついた部分の面積は何cm 2 ですか。 この問題は、下図のように変形することができ、一辺が1cmの正方形6個分になるので、答えは 6cm 2 。Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube
十边形 随意优惠券
正10角形 内角の和
正10角形 内角の和-正十角形の作図 正10角形は、正5角形の外接円と、その一辺の二等分線が交わる点を求める方法で作図します。 正十一角形の作図 正11角形。連結式奇数等分器の部分を5枚使います。十文字の照準線の長い部分を重ねる方がいいと思います。10角形:10,10,10,5の計35 となります。 正n角形の頂点をそれぞれ区別する場合、全種類の対角線はn本存在します。



正16边形图片 第1页 一起扣扣网
難関大学で頻出テーマの正\(n\)角形ですが、意外とその対処法を知らない受験生は多いです。この記事を読んで、その対処法を完璧にしてしまいましょう! 三角形に分割せよ 正\(n\)角形を前にしてすべきことは、ただ1つです。 Point あ 正\(n\)角形 → \(n\)個の三角形に分割 \(n\)個の三角形に分割正10角形準結晶のHAADFsTEMか らNi,Ruの 原子が識別され た結果を付け加える。 2正10角 形準結晶の構造の特徴1) 正10角形準結晶の構造は,一 般に正10角形を断面とするカラム状 原子クラスターが2次 元的に準周期配列した構造と特徴づけること全5種類の正多面体(正四面体・正六面体・正八面体・正十二面体・正二十面体)のデータです。それぞれの多面体は 直径10cmの球に内接する大きさ になっています。 正4面体 ダウンロードtetrahedronpdo (3KB) 正6面体 ダウンロードcubepdo (4KB) 正8面体
中学生の時の話です。 小学生までは三角定規とコンパスで正三角形や正方形、六角形を書く方法などを学びます。 中学生になると、こんどは分度器を使って正n角形を書くことを学びました。このとき書けるのは、正三角形、正四角形正17角形の作図ファイルは、15年くらい前に、 「シンデレラで学ぶ平面図形」阿部一志(シュプリンガー・フェアラーク東京) の記事から作成しました。今回、GeoGebra を始めて使ってみたので思い出して作成してみました。正10角形 \2\sin(\pi/10) = \frac{1\sqrt{5}}{2}\ となります。正5角形よりシンプル。 実は正10角形は正5角形の作図がどうやって行われるかが理解できていると簡単に求めることができます。
三角形~二十角形までの正多角形を描くことができます。 テンプレート図形を使うと簡単に描けます。 正多角形は、テンプレート図形の基本図形のグループにあります。 端から描く;三角形~二十角形までの正多角形を描くことができます。 テンプレート図形を使うと簡単に描けます。 正多角形は、テンプレート図形の基本図形のグループにあります。 端から描く;全5種類の正多面体(正四面体・正六面体・正八面体・正十二面体・正二十面体)のデータです。それぞれの多面体は 直径10cmの球に内接する大きさ になっています。 正4面体 ダウンロードtetrahedronpdo (3KB) 正6面体 ダウンロードcubepdo (4KB) 正8面体



正邊形 几何术语 资讯 这是什么


十边形 随意优惠券
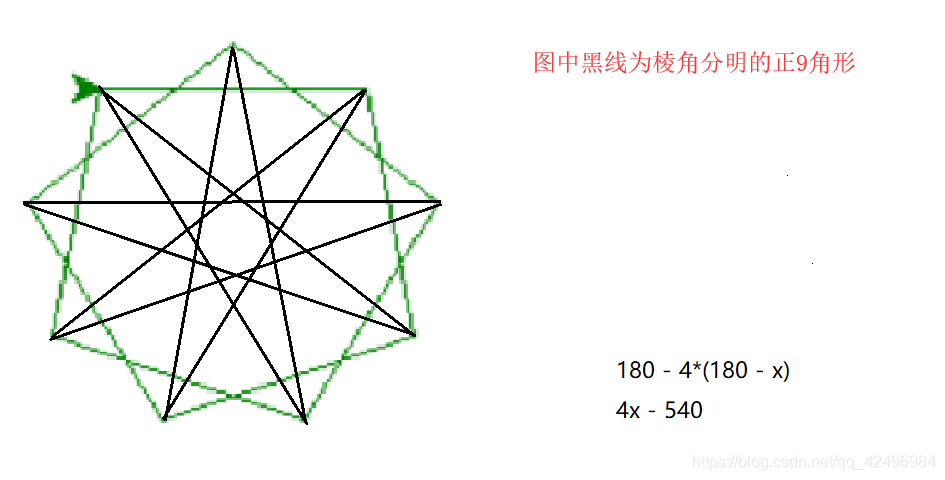
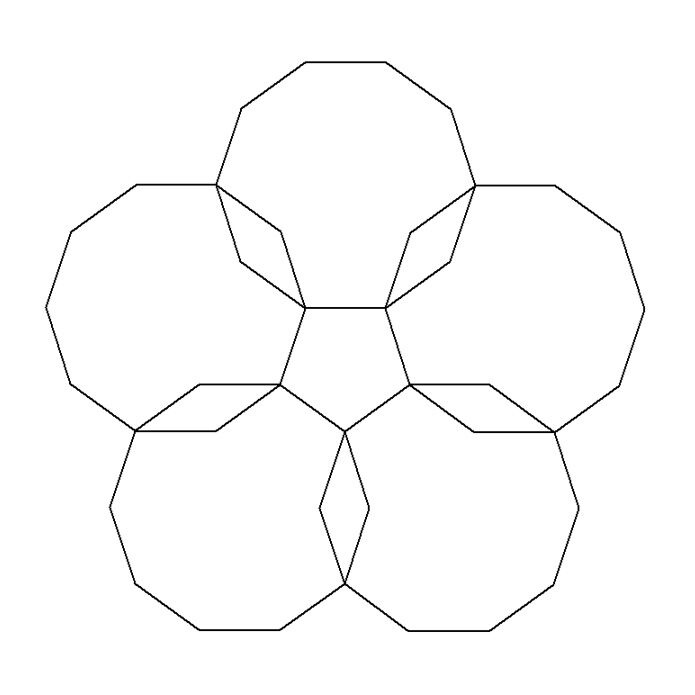
正5 角形が並んでできる穴の縁である図形(正10 角形)の1つの外角は、上の図から 5 に なっている。どの外角も、これと同じ状況であるから、この穴の縁を歩いている人が、m 個の角 で進行方向を変化させる角度の合計は、 5 £ m となる。AlNiRh系正10角形準結晶の5次元構造解析 H28 修士課程修了 MnCrNiSi系正12角形準結晶の形成に関する時効効果 H27 修士課程修了 AlPdRu系における直方晶近似結晶と正10角形準結晶の形成条件・構造関連性 H26 修士課程修了 Mn基合金における正12角形準結晶の形成正10角形準結晶の構造は,一 般に正10角形を断面とするカラム状 原子クラスターが2次 元的に準周期配列した構造と特徴づけること ができるす なわち,2次 元平面で見れば,カ ラムの断面である正 10角形が,辺 共有と時にはそれに貫入した結合(つ ぶれた6角 形を


求风筝图形内角度数 为什麽角2 角4如图案所示 2 4 5个风筝形拼成一个正10边形 所以 1 10 2 180 10 8 180 144 5 3 360 3 72 风筝形是个四边形 内角和是360度 并且 2 4 所以 作业 慧海网


尺规作图 正三边形到正十七边形 知乎
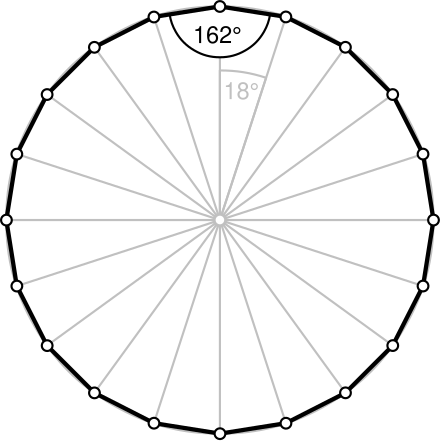
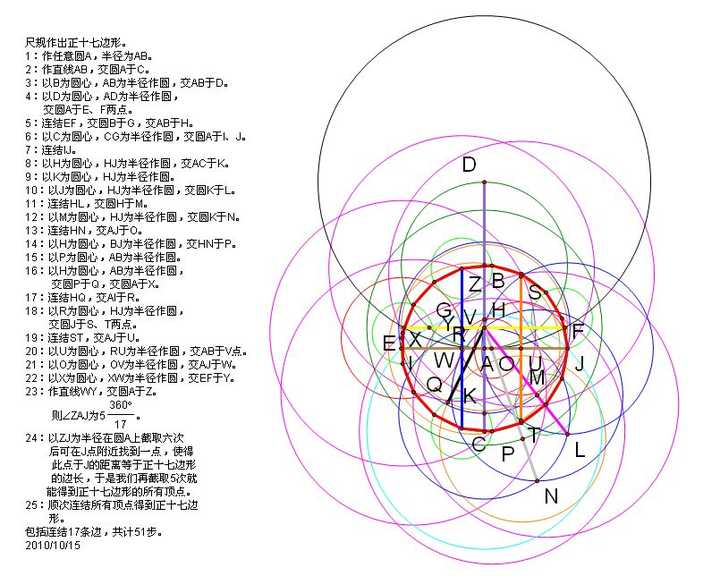
性質 正十七角形においては、中心角と外角は約2118°で、内角は約158°となる。 また、一辺の長さが a である正17角形の面積は ≈ である。 作図 正十七角形は定規とコンパスによる作図が可能な図形の一つである。 p が素数である正p角形のうち、このような作図が可能なものは p が正10角形 \2\sin(\pi/10) = \frac{1\sqrt{5}}{2}\ となります。正5角形よりシンプル。 実は正10角形は正5角形の作図がどうやって行われるかが理解できていると簡単に求めることができます。まずは正十角形の外角1つ分の大きさを求めます。 $$360 \div 10=36°$$ 内角は\(180(外角)\)より $$=144°$$ となります。 内角の和を考えて求める場合には $$180 \times (102)=1440°$$ 内角の和をこのように求めて 10で割ってやれば求めることができます。 $$1440 \div 10


いろいろな立体の問題



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information
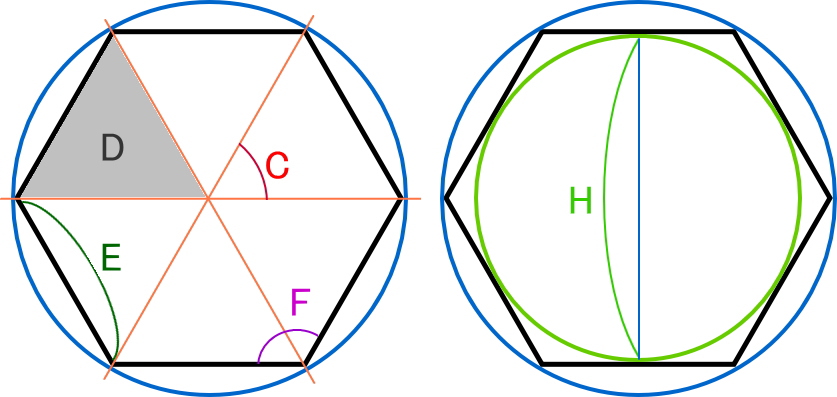
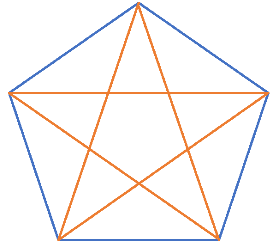
(10−3)×10÷2=35で、正十角形の対角線の本数は35本ということがわかります。 このように、正n角形の対角線の本数は(n−3)×n÷2で出すことができるのです。 ぜひ覚えておいてくださいね。 (963文字)正多角形の内角の和っていくつ?? 正多角形の内角をぜーんぶ足したらナビゲーションに移動 検索に移動 正十角形 十角形 (じっかくけい、じっかっけい、 英 decagon )は、 多角形 の一つで、 10 本の 辺 と 頂点 を持つ 図形 である。 内角 の 和 は1440°、 対角線 の本数は35本である。 正十角形においては、 中心角 と 外角 は 36 ° で、内角は 144 °となる。 一辺の長さが a の正十角形の 面積 S は、 S = 5 2 a 2 cot π 10 = 5 a 2 2 5 2 5 ≃ 7正十七角形 基本的には 正五角形の作図 と全く同じ議論を使いますが,正十七角形の作図法はもっと複雑になります.議論の意味自体がよく分からない場合は, 正五角形の作図 に戻って復習してください.『作図可能である』という性質の一番のポイントは,途中の中間体が二次拡大(二次



難しい多角形を定規だけで描く方法 交点から線で結ぶ Alumania Information



正七边形画法视频 尺规作图正七边形 正八边形 正九边形 Www Dingjisc Com
Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと思います。



如图 1 将一张正六边形纸沿虚线对折折3次 得到一个多层的60 角形纸 用剪刀在折叠好的纸上随意剪出一条线 如图 2 雨露学习互助


正 角形 正多角形 を表にしてみる エクセル関数の使い方


C 圆 Circle 图灵社区


看完这些正多边形的尺规作图方法 你还不认为数学也是一种艺术吗



正多边形形状十字形角度 圆形png剪贴画白色 单色 多边形 黑色 单免抠素材下载 图片id 其它元素 Png素材 素材宝scbao Com


看完这些正多边形的尺规作图方法 你还不认为数学也是一种艺术吗


実践例 プログラミングで正多角形を学ぶ 山﨑智仁 Tomohito Yamazaki Note


用正方形纸片折出等边三角形 Matrix67 The Aha Moments



正八边形怎么画 Www Dingjisc Com


正多角形 算数用語集


十边形 维基百科 自由的百科全书


正十八边形 Www Shianwang Com


パ 正十角形分割答え2個 いわいまさかチャンネル



十一边形 维基百科 自由的百科全书
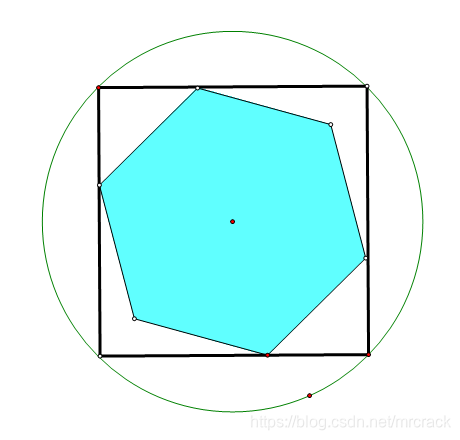


打赏评论 收藏点赞 分享文章 微博qq 微信 Osc U1w6ntu7的个人空间 正文 Codeforces 1354c2 Not So Simple Polygon Embedding 几何画板 转 O Osc U1w6ntu7 发布于 05 12 12 字数365 阅读74 收藏0 点赞0 评论0 C Educational Codeforces Round
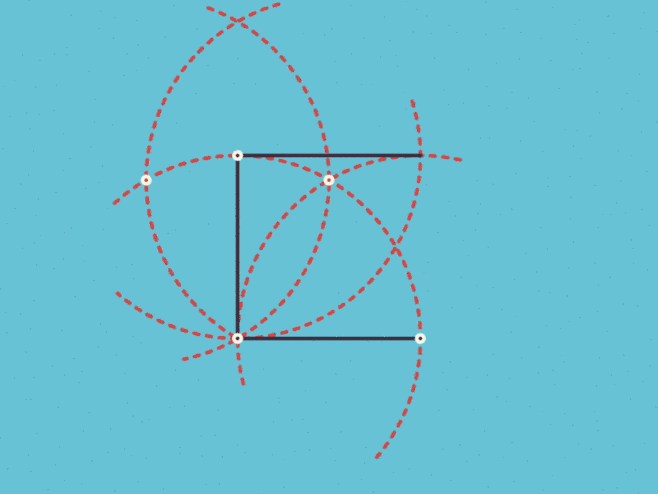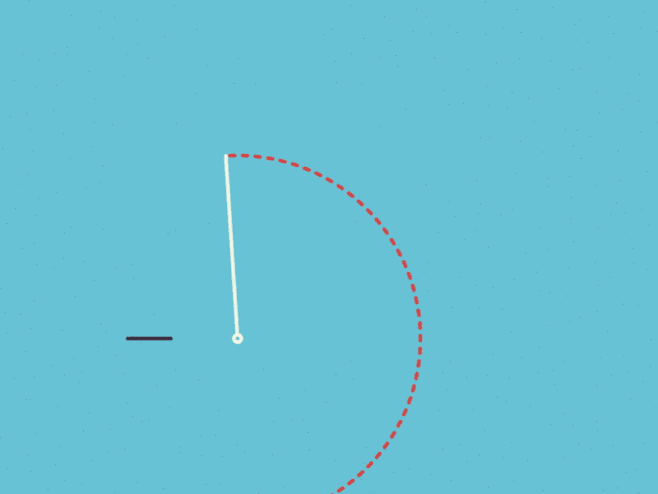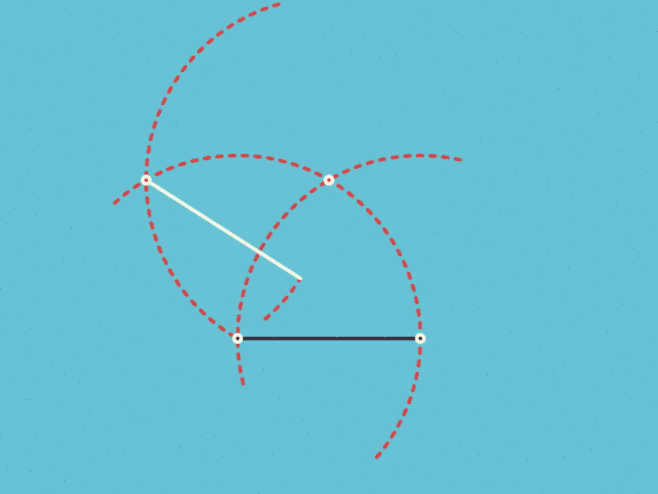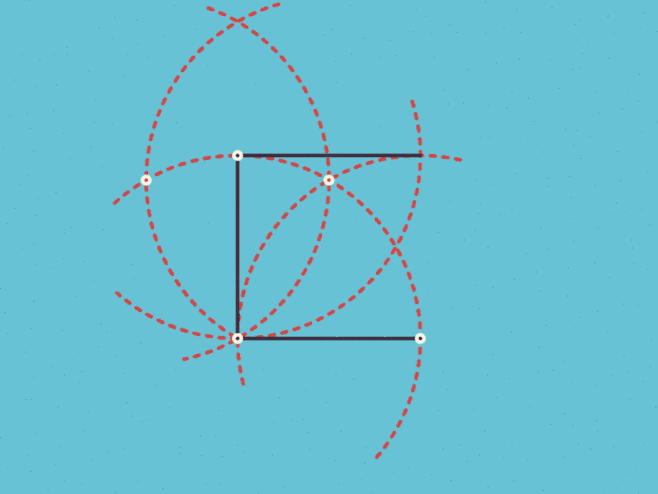


尺规作图 正三边形到正十七边形 知乎



数学尺规作图 8 正10边形 哔哩哔哩 つロ干杯 Bilibili
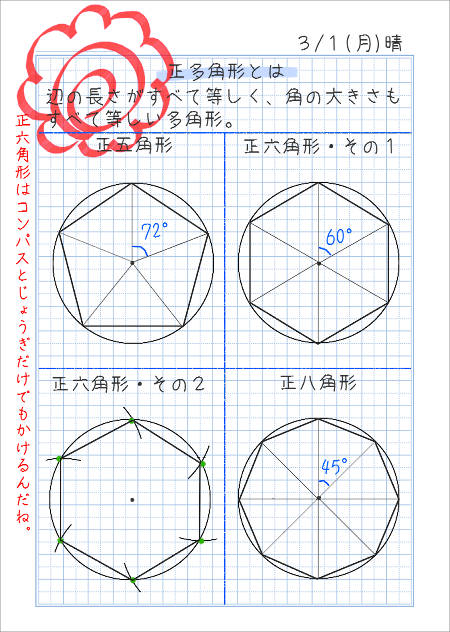


いろいろな正多角形をかいてみよう 家庭学習レシピ



五千三百六十一边形 伪基百科



立体十角形 の普遍的構造 真理探究と歴史探訪 楽天ブログ



正40边形尺规作图 第1页 一起扣扣网


過去の表紙44



十一边形 Wikiwand



三角形の個数と組み合わせの問題です 高校数学に関する質問 勉強質問サイト


宮崎市 放課後等デイサービス 児童発達支援 しんがくどう 正六万五千五百三十七角形 人の環 テーマ 人


正七角形の作図 教材作家



两个小学生的12边形烧脑题 每日头条


智慧幾何聯盟



十六边形 维基百科 自由的百科全书



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
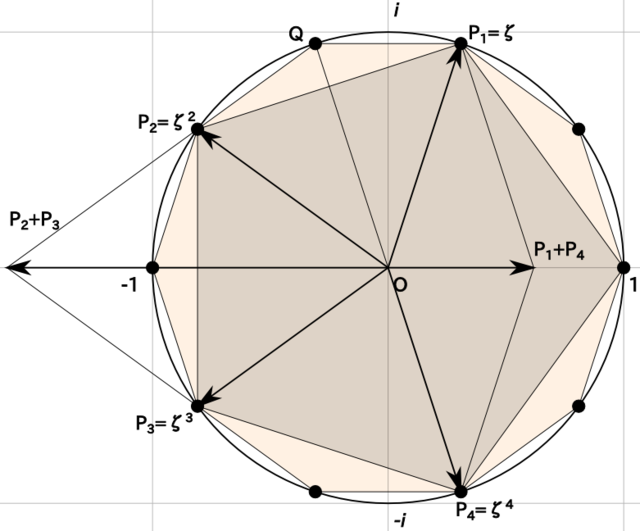


半径1の円に内接する正n角形の一辺の長さ 元祖ワシ的日記



打赏评论 收藏点赞 分享文章 微博qq 微信 Osc U1w6ntu7的个人空间 正文 Codeforces 1354c2 Not So Simple Polygon Embedding 几何画板 转 O Osc U1w6ntu7 发布于 05 12 12 字数365 阅读74 收藏0 点赞0 评论0 C Educational Codeforces Round
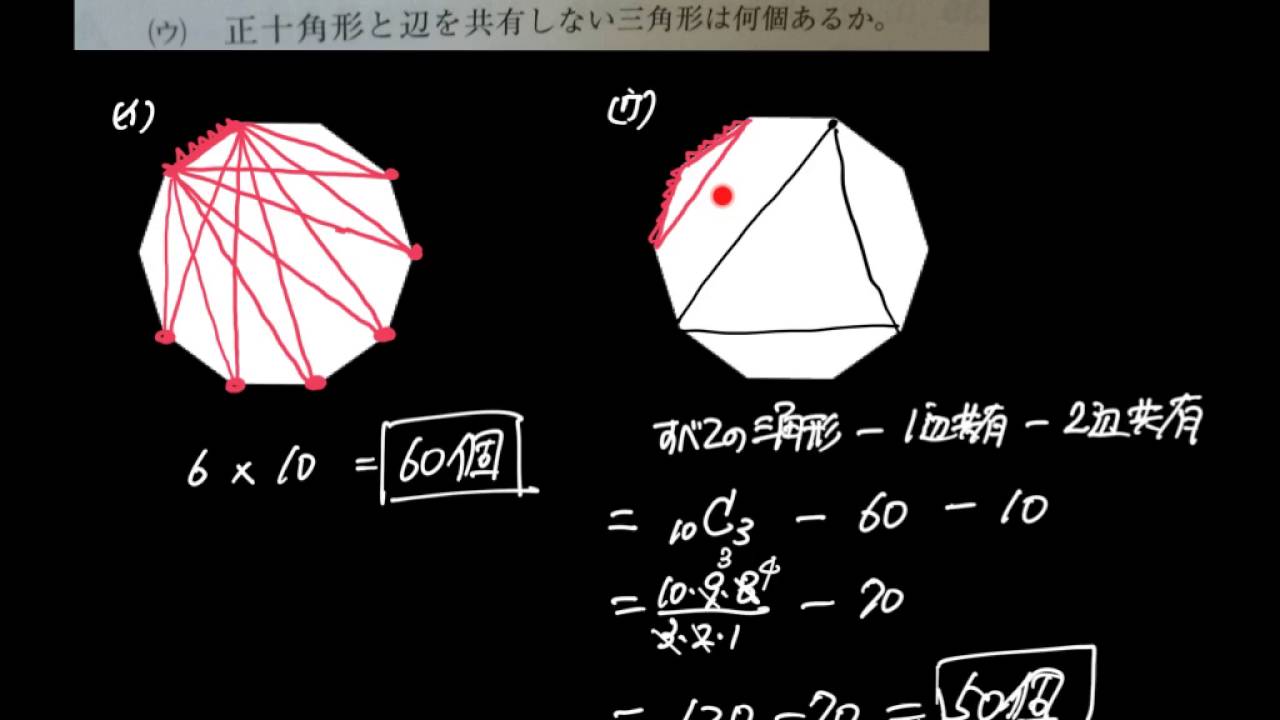


数a 正10角形 一辺を共有する三角形 Youtube


正十角形出るとオモタよ ジュニア算数オリンピック18 父ちゃんが教えたるっ
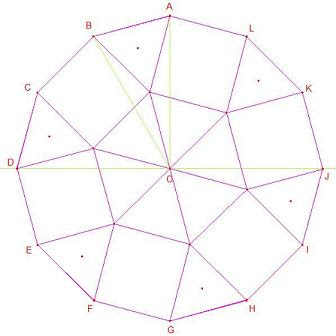


ラブリー正12 角形 ただぬりえ



多边形几何 五边形 六边形和十二边形


数学尺规作图 3 正5边形 哔哩哔哩 つロ干杯 Bilibili



尺规作图正10边形 第1页 一起扣扣网



十角星 Wikiwand



3种方法来求五边形的面积
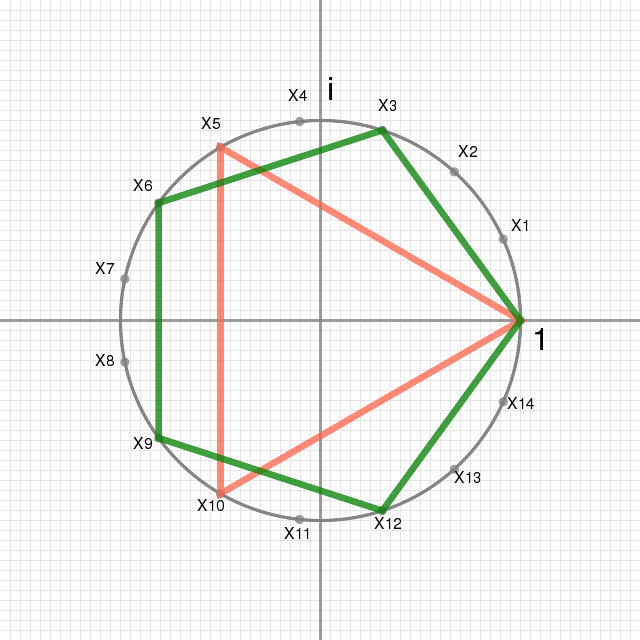


正15角形 元祖ワシ的日記



两个小学生的12边形烧脑题 每日头条


数学尺规作图 8 正10边形 哔哩哔哩 つロ干杯 Bilibili



十一边形 Wikiwand


尺規作圖正多邊形


高斯墓碑正十七边形高斯的墓碑中有 正十七边形 吗其墓碑是怎样的 学习岛


Scratch3数学之美01 绘制正多边形 简书



正16边形图片 第1页 一起扣扣网


六边形 Wikiwand


看完这些正多边形的尺规作图方法 你还不认为数学也是一种艺术吗


トップ正10 角形 壁紙おしゃれトイレ


ラブリー正10 角形 ただぬりえ


数学尺规作图 8 正10边形 哔哩哔哩 つロ干杯 Bilibili



在素描中画正十二面球体技巧画法



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


街角の数学 Street Wasan


正16边形图片 第1页 要无忧健康图库



10 正十角形 Youtube


多边形的中英文名称大全 英国羽西
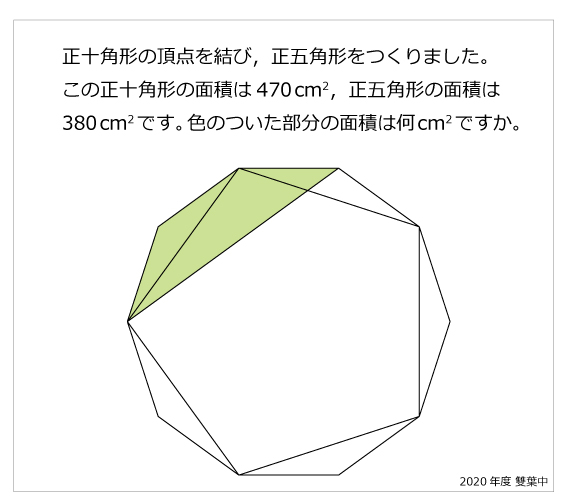


今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦


正十角形abcdefghijにおいて Afとcgの交点をpとするとき 角a Yahoo 知恵袋



正多边形 属性



十边形的画法步骤图 第1页 一起扣扣网
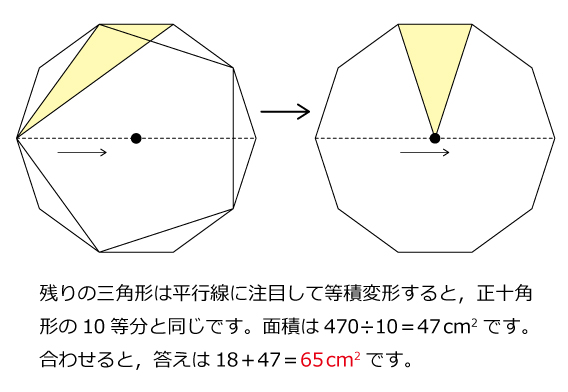


今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦



十角形 Wikipedia



12面体をメロンパン3で作っている時 この立体の線を辿っていくと どの線も立体をぐるりと一回りしていることに気が付いた ぐるり一回りで正10角形を作っていること そしてそれが球体の大円 地球で言えば赤道のように最大半径の トーラス 球体 体


数学の質問です 正十角形の3この頂点を結んで三角形をつくる 問正十角形と1 Yahoo 知恵袋


コンパスと定規を使った七角形 正多角形 の描き方 図形の描き方016a 夏貸文庫



高斯墓碑 高斯墓碑正十七边形 高斯的墓碑图片 高斯墓碑正十七角星



正十边形尺规作图画法 第1页 一起扣扣网



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


直觉泵和其他思考工具36 什么是基因基因就像软件中的子程序



没有圆规怎么找圆心 三人行教育网 Www 3rxing Org



规尺半圆弧六等分 三人行教育网 Www 3rxing Org



高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月



八年级下册第五章平行四边形5 1多边形同步练习1下载 在线阅读 爱问共享资料


智慧幾何聯盟


Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


二十边形 Wikiwand


正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生のメカニズム


対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に


高斯作出正17 边形的依据是什么 知乎



如何求正多边形的面积 7 步骤


用正方形纸片折出等边三角形 Matrix67 The Aha Moments



二十四边形 Wikiwand



正多边形 维基百科 自由的百科全书



つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



正十角形の書き方 ひだまりママのブログ



内角和 内角和公式 五边形内角和 N边形内角和公式



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


青少年编程 用python探究数学 3 老齐教室


十角館の妄想再現建築 Part2 壁作り ひもの まいくらいふ



0 件のコメント:
コメントを投稿